Skip to content

决策树学习笔记

Info

作者：Vincent，发布于2021-08-28，阅读时间：约7分钟，微信公众号文章链接：

1 前言

决策树是非常经典的机器学习模型，日常工作中许多分类和回归问题都可以用决策树解决，很多更高级、先进的机器学习模型也基于决策树构建，为了夯实基础、正确运用决策树，今天我们来回顾一些决策树里最重要的技术细节。

鸢尾花品种分类决策树示例

2 算法重要细节

2.1 如何做预测

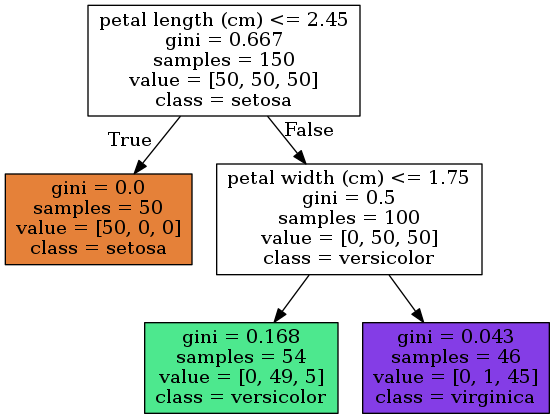
示例中深度为2的决策树的展示了做决策的过程和结论，对于150个样本点，在根节点上，决策树以花瓣长度（petal length）是否小于2.45厘米将数据分成两部分，花瓣长度小于2.45厘米的样本被分类成setosa，大于2.45厘米的数据继续以花瓣宽度（petal width）是否小于1.75厘米进行分类，小于的部分被认为是versicolor，大于的部分则是virginica。

图中的samples即为这个大类中的样本数量，如深度为1的左侧叶子节点中samples=50意味着花瓣长度（petal length）小于2.45厘米的样本有50个。而value则代表当前节点中训练数据的分布，如深度为2的左侧绿色节点中[0, 49, 5]表示这个节点中，有0个setosa，49个versicolor和5个virginica，总共54个samples。

2.2 预测的依据

在示例的决策树中，还要一个重要的指标叫做Gini - 基尼系数，这个系数衡量当前节点的不纯净度（impurity），直观来说，当一个节点里的所有样本都属于同一类时，节点的纯净度最高，基尼系数为0。Gini的定义为

Gini

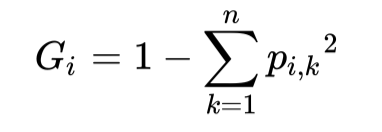
其中\(P_{i,k}\)是在i个节点中k类的样本占总体样本的比例。比如示例中深度为2的右侧节点的Gini为\(1-(0/46)^{2}-(1/46)^{2}-(45/46)^{2} ~= 0.043\)。以最常用的Python机器学习库Scikit-Learn(v0.24.2)中的DecisionTreeClassifier类为例，其在实现分类和回归树（Classification and Regression Tree, CART）时，在选择分裂节点的过程中，决策树选择分裂节点和阈值的依据即与Gini有关。其优化目标（损失函数）如下所示：

CART分类损失函数

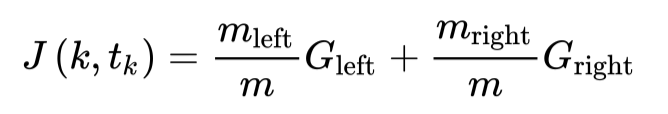
其中\(G_{left/right}\)分别为左侧和右侧节点的Gini，而\(m_{left/right}\)分别为左侧和右侧节点的样本数量。CART算法会做贪心搜索（Greedy Search），从根节点开始分裂，并在层层子节点中搜索能够有效减少Gini的特征和阈值，直到分裂的层数到达最大深度（由max_depth参数定义）或已经找不到能够减少Gini的节点。直观来说，找到最好的树是一个NP-complete问题，因此算法最终只会找到一个相对好的方案，而非最好的解决方案。

除了Gini之外，熵（Entropy）也可以用来衡量分裂节点的效果，用以衡量混乱度，在决策树的节点中，当一个节点里的样本都属于同一类时，熵的值为0。其定义如下：

熵（Entropy）

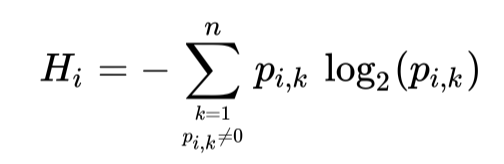
其中\(P_{i,k}\)是在i个节点中k类的样本占总体样本的比例。比如示例中深度为2的右侧节点的熵为\(-(1/46)log_{2}(1/46)-(45/46)log_{2}(45/46) ~= 0.151\)。在Scikit-Learn(v0.24.2)中使用DecisionTreeClassifier类时，可以通过设置criterion参数为entropy来使用熵作为衡量指标。但通常使用gini和Entropy得出的树差别不大。主要的区别在于Gini计算更快，并且使用Gini会让树将样本更加集中地划分到节点里，而使用Entropy会让样本在树的分布更加均衡。

2.3 防止过拟合

决策树本身几乎没有假设，同时不依赖于特征缩放（Feature Scaling），但模型本身是需要加约束防止过拟合。可以通过控制模型参数达到正则化的目的。以Scikit-Learn(v0.24.2)中使用DecisionTreeClassifier类为例，下列参数常用于实施正则化防止过拟合：

  • max_depth：树的最大深度，默认值是空，意味着树的最大深度不受限制。
  • min_samples_split：分裂一个节点前所需的最小样本数，默认值为2。
  • min_samples_leaf：一个叶子节点最少所需的样本数量，默认值为1。
  • min_weight_fraction_leaf：默认值为0。当设置了class_weight后，样本权重不同，而该参数则约束叶子节点中权重占总体样本的比例，大意和min_samples_leaf类似，但用比例表示。
  • max_feature：分裂节点时考虑的特征数量，默认为考虑所有特征。注意，决策树在找到一个有效的分裂节点前不会停止搜索，即便是搜索的特征数量已经超过了max_feature设定的值。
  • max_leaf_nodes：叶子节点数量的上限，默认值为空。
  • min_impurity_decrease：分裂一个节点所需减少的最低不纯净度，默认值为0。

通常，增加min_参数或者减少max_参数有助于决策树的正则化。

2.4 回归任务

在Scikit-Learn(v0.24.2)中可以使用DecisionTreeRegressor类来执行回归任务。

回归树

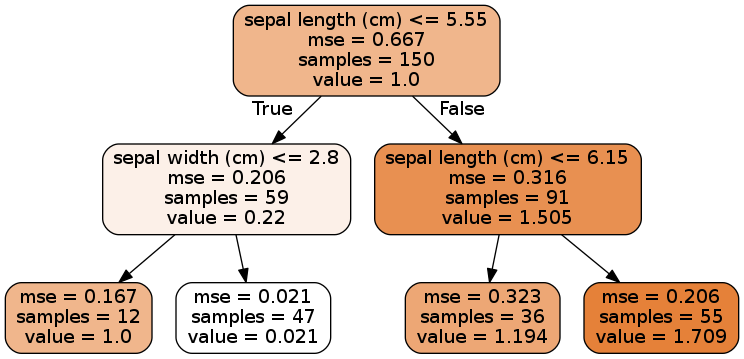
此时预测值是叶子节点里样本目标值的均值。做回归任务时，CART算法实施方式和分类基本一致，只不过此时优化的目标是减少与目标值的均方差（Mean Squared Error, MSE）

回归树的损失函数

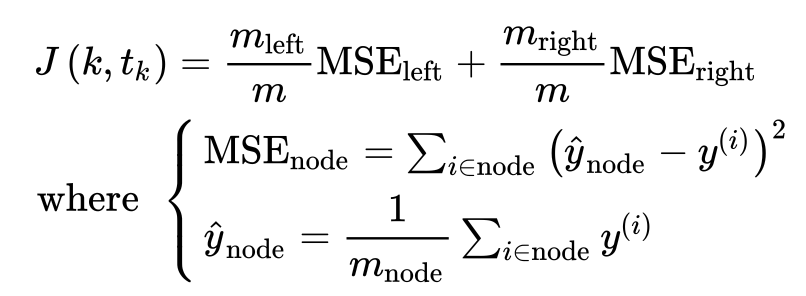
回归树模型参数基本与分类数模型参数一致，可以通过类似的办法防止模型过拟合。

2.5 其他重要属性

Scikit-Learn的实现中，决策树的feature_importances_属性能展示特征的重要性，其依据是各特征对于衡量指标的减少量，返回归一化后的值。如果特征中不同值的数量非常多（高数量类别属性，High Cardinality Features），推荐使用sklearn.inspection.permutation_importance。

如果要对树进行手动调整如改变分裂的阈值，可以使用sklearn.tree._tree.Tree。

3 总结

决策树应对分类和回归问题有不错的表现，但也存在一些限制和弱点，如对于数据的方向性和波动较为敏感，这些问题一棵树难以完美解决，那多种几棵树是否有更好的表现呢？下回我们聊聊随机森林！

示例代码：

# 依赖包
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import DecisionTreeRegressor
from sklearn.tree import export_graphviz

import matplotlib.pylab as plt
import numpy as np


# 导入示范数据
iris = load_iris()
X = iris.data[:,:2] # 选择花瓣长度和花瓣宽度作为特征
y = iris.target

# 查看数据分布
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
plt.show()

# 建设一颗决策树
tree_clf = DecisionTreeClassifier(criterion='entropy', max_depth=2)
tree_clf.fit(X, y)

# 导出决策树图形
export_graphviz( tree_clf,
out_file="iris_tree.dot",
feature_names=iris.feature_names[:2],
class_names=iris.target_names,
rounded=True,
filled=True
)

# 决策边界绘制函数
def plot_decision_boundary(model, x):
    #生成网格点坐标矩阵,得到两个矩阵
    M, N = 500, 500
    x0, x1 = np.meshgrid(np.linspace(x[:,0].min(),x[:,0].max(),M),np.linspace(x[:,1].min(),x[:,1].max(),N))
    X_new = np.c_[x0.ravel(), x1.ravel()]
    y_predict = model.predict(X_new)
    z = y_predict.reshape(x0.shape)
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.pcolormesh(x0, x1, z, cmap=custom_cmap)

# 绘制决策边界
plot_decision_boundary(tree_clf, X)
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
plt.show()

# 查看特征重要性
print(tree_clf.feature_importances_)
Viewed times

Comments